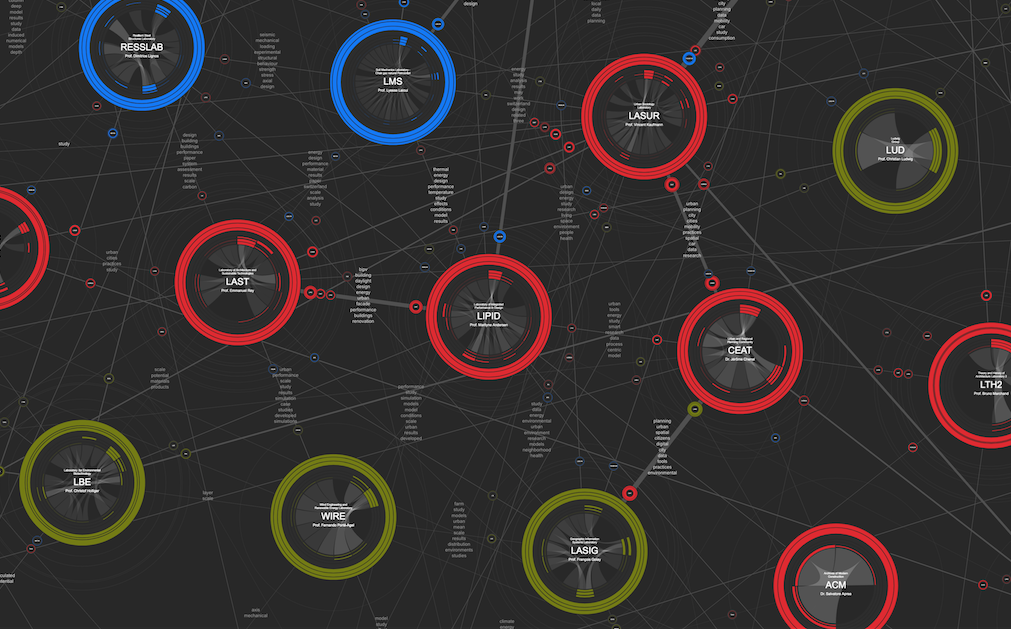
Hexagons, Satellites, and Semantic Background
by Dario Rodighiero
on November 16, 2018
Network visualizations are objects that are very stable from a graphical point of view: nodes and relations are represented as circles and lines that usually present textual and quantitative information. This visual method adopted by the large part of scientists was introduced during 1930s by the sociologist Jacob L. Moreno who published a book where networks were employed to illustrate social ties. Although different efforts were done to improve the arrangement and temporal dimension of networks, the graphical representation timidly advanced in almost one century. How to enrich further the visual grammar of networks?
This presentation introduces three visual elements that are intimately allied and can be used in any network visualization: hexagons, satellites, and semantic background. These elements advance the visual grammar of network visualizations enriching interactivity, aesthetic, and information amplification. 1) The hexagonal tiling introduces a pattern by arranging nodes at the same distance in a never-ending rhythm. 2) The satellites refer to connections by spinning around each node; unlike the lines that usually represent relations, the satellites can display the heterogeneity and the distance of connections. 3) The semantic background fills in the regular space created by the hexagonal tiling by placing textual information between nodes whether there exists a relation or not. The usefulness of hexagons, satellites, and semantic background will be demonstrated through a specific case study called Affinity Map. This visualization is available on the Internet at https://affinitymap.epfl.ch.
About Dario Rodighiero
Dario Rodighiero is a digital humanist deeply versed in design practice. He is a postdoctoral research fellow at EPFL and member of the Laboratory of Digital Humanities directed by Frédéric Kaplan. His work focuses on the visual representation of individuals, especially on the mapping of academic collectives and their dynamics.
@dariorodighiero